Eric Hwang
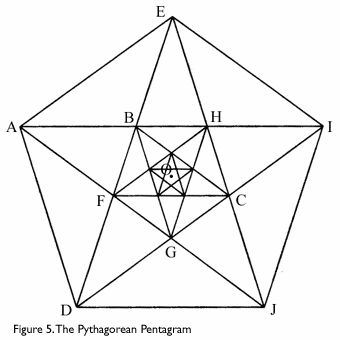In Figure 5, ABCD is a Penrose kite and ABCE is a Penrose dart. To prove this, we must show that they are both kites with ∠ADC and ∠AEC measuring 72° and ∠ABC measuring 144°. Since the pentagon is regular, ∠AOD ≅ ∠ADJ = 72°, and ∠AED ≅ ∠DEJ = 36°. Also, since triangles ABE and CHB are similar, ∠BAE ≅ ∠HCB. So triangles ABE and CBE are congruent, and AE ≅ CE, and ∠AEC = ∠AEB + ∠BEC = 72°. Similarly, triangles ABD and BDC are congruent, and ∠ADC = 72°.
To enforce the non-periodic tiling, the tiles can only be joined in certain ways. For example, it would be simple to join them so that they form the rhombus and tile periodically. To make sure kites and darts are joined in legal ways, two circular arcs are drawn on each figure, and two edges can only be adjacent if the joining arcs are the same color.
Placing darts and kites around a vertex and then expanding radially can create a Penrose pattern. Sometimes the piece to be added is forced, and at others, it is not. For example, the concave part of a dart forces two kites to form an “ace” (Figure 6).
The ratio of kites to darts in a Penrose tiling is the golden ratio, as is the ratio of the area of a kite to a dart. The golden ratio, t = (1 + √5)/2, is a number that has the characteristics that for any rectangle that has dimensions in the golden ratio, if a square is cut off, the remaining rectangle has the same shape as the original, so (t-1) / 1 = 1 / t.
The fact that the ratio is irrational is the underlying principle in the proof that the tiling is non-periodic, since the ratio would be rational in a periodic tiling. If the tiling were periodic, the ratio would be the same in every one of the infinitely repeating patterns, so only one representative pattern would need to be investigated. Since this pattern is finite in size, it contains a finite number of polygons, so the relationship can be represented as a ratio of integers, which is rational.
Not only are Penrose tilings non-periodic, but there are also an infinite different tilings that can be made with each set of Penrose tiles. The proof of this relies on John Horton Conway’s concept of “inflation” and “deflation.” To inflate a Penrose tile, cut every dart in half down its axis of symmetry,
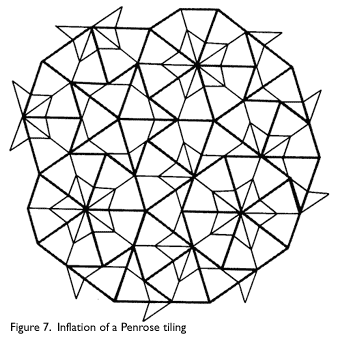and glue all of the shorter ends of the original polygons together. The resulting pattern (Figure 7) is another Penrose tiling with larger kites and darts, and is different from the original pattern. In this diagram, the inflated pattern is represented by the thicker lines. Since the new pattern is also a Penrose tiling with kites and darts, it can be inflated to another Penrose tiling using even larger kites and darts. This procedure can be repeated an infinite number of times, and a similar process of deflation, finding smaller Penrose tilings, can also be performed an infinite number of times.
Inflation can be used to show that the ratio of kites to darts approaches the golden ratio as the plane approaches infinity. Let K represent a kite, and D represent a dart. Let K′ represent a composed kite in a one-step inflation, and D′ a composed dart. Since an inflated kite is composed of two kites and two half-darts, and an inflated dart is composed of one kite and two half-darts, we get the two equations
K′ = 2K + D; D′ = K + D
which gives the following linear system:
Similarly,
K″ = 2K′ + D′ = 5K + 3D
D″ = K′ + D′ = 3K + 2D
which results in the linear system
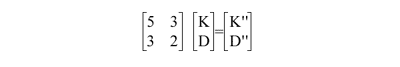
The matrix is in the form of M = P2k, where k is the number of inflations from the initial tiling, and P is the Fibonacci matrix. Since the ratio Fm/Fm-1 approaches the golden ratio as m approaches infinity in a Fibonacci sequence, the ratio of kites to darts also approaches that as k approaches infinity.