Eric Hwang
For many years, it was believed that a set of tiles that tiled only non-periodically could not exist. In 1961, Hao Wang tried to find different ways to tile various unit squares called Wang dominoes, whose edges were colored differently. Wang tried to see if any set of Wang dominoes would tile so that adjacent edges shared the same color, and thought that any set of tiles that could tile the plane could do so periodically. Robert Berger showed in 1964 that Wang’s conjecture was false, and found a set of 20,000 Wang dominoes that tiled only non-periodically. He was later able to reduce this number to 104, and Donald Knuth found a set of 92 Wang dominoes that tiled non-periodically. How does this relate to the non-periodic tiling of polygons? It is easy to convert Wang dominoes into polygons that tile only non-periodically by putting edges and slots in the sides, similar to a jigsaw puzzle. Raphael Robinson and Robert Ammann found different sets of six tiles that force non-periodic tiling, and although it has not been proven, it is strongly believed that this is the smallest number of square shaped tiles that will force non-periodic tiling.
At the University of Oxford, Roger Penrose investigated sets of tiles that were not square in shape that would force non-periodic tiling. He found a set of six tiles in 1973 (Figure 1), and in 1974 found a set of four tiles. Soon after that he found a set of two tiles that would force non-periodic tiling. Penrose tiles can be pairs of several different shapes, though the two most interesting, and most often studied by John Horton Conway, are those depicted in Figure 2b, known as “darts” and “kites.”
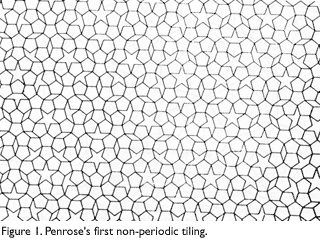The darts and kites can be obtained from a rhombus with degree measures of 72° and 108° by dividing the long diagonal into two segments in the golden ratio f = (1+√5)/2 = 1.618… then joining the dividing point to the obtuse corners as shown in Figure 2a. Both rhombuses are composed of two golden triangles, the first having sides with ratios of 1:f:f, and the other having sides with ratios of 1:1:f. The ratio of the areas of the kite and dart is the golden ratio as well. The area of a kite is proportional to the product of its diagonals and one of the diagonals of the kite has equal length to one of the dart’s diagonals. So the areas are proportional to the other diagonal, which we set to be the golden ratio when constructing the kite and dart.
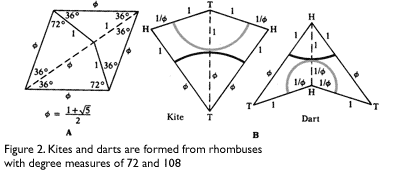The other common polygons used in Penrose tilings are Penrose rhombs, which are also composed of golden triangles. One rhomb has degree measures of 72 and 108, while the other has degree measures of 36 and 144. Since both sets can be derived from golden triangles, it makes sense that a kite and dart tiling can be translated into a rhomb tiling, and vice versa (Figure 3).
The darts and kites and Penrose rhombs can be constructed using a straightedge and compass as follows. First, construct a regular pentagon. To do this, take a circle with center O and a given diameter with one endpoint labeled P0 (see Figure 4).
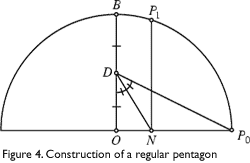Construct the perpendicular bisector of the diameter that intersects the circle at point B. Next, bisect segment OB, and call the midpoint D. Draw DP0. Next, construct the bisector of ∠ODP0, which intersects the diameter at point N. Next, construct the perpendicular to the diameter through N which intersects the circle at point P1. P0 and P1 are two of the pentagon’s five vertices. Now, if all of the vertices are connected in all possible ways, the Pythagorean Pentagram (Figure 5) is obtained. The kites and darts and the Penrose rhombs can both be constructed from the Pythagorean Pentagram.