Eric Hwang
Since the darts and kites are composed of golden triangles, it is not surprising that Penrose tilings exhibit approximate or exact five-fold symmetry, as the golden ratio is integral in the construction of a regular pentagon. There are seven ways to arrange darts and kites around a vertex in a Penrose tiling, and only two of them have perfect pentagonal symmetry. The first, called the sun, is composed of five kites around a vertex. If pieces are added to the sun so that symmetry is preserved, the “infinite sun” pattern shown in Figure 8a is obtained. The other symmetric arrangement is composed of five darts around a vertex, known as the star pattern, shown in Figure 8b.

The five darts around the vertex force ten kites and form five aces, and the pattern expands from there. The Sun and Star patterns are the only Penrose patterns that exhibit true five-fold symmetry, and the two are equivalent in that the inflation or deflation of one results in the other (inflating or deflating an infinite sun pattern results in an infinite star pattern).
For instance, take the infinite Sun pattern. By the rules of inflation, the five kites in the center would each be added to the two half-darts each one is adjacent to, forming five darts in the center. Proceeding outward, the 20 kites in the next concentric ring pair up and combine with two half-darts to form a ring of 20 larger kites immediately surrounding the five new darts. The inflation continues and the infinite Star pattern is obtained.
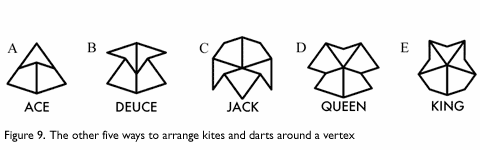
The other five are as follows: the ace (Figure 9a), the deuce (Figure 9b), the jack (Figure 9c), the queen (Figure 9d), and the king (Figure 9e). There are also seven vertex neighborhoods using the Penrose rhombs, as shown in Figure 10. Only one of them leads to perfect symmetry (Figure 10.2), though there are two ways to symmetrically tile the plane around it.

While only the star and sun have five-fold symmetry, all Penrose patterns form patterns determined by five families of parallel lines that cross the plane in five different directions and intersect each other in 72° angles. One family, known as Ammann Bars, shown in Figure 11, is constructed so that the lines cross the concave corners of darts that point in the same or opposite direction. The spacings between Ammann bars fall into one of two lengths which are in the golden ratio. Also, the ratio of long spacings (L’s) to short spacings (S’s) is also in the golden ratio on the infinite plane, and the sequence of L’s and S’s is non-periodic, providing a one-dimensional analogue of the Penrose tiling.

The general five-fold symmetry of Penrose tiles is not surprising when we remember that the tiles can be obtained from regular pentagons.
