Eric Hwang
The kites and darts can be changed into other shapes as well, as Penrose showed by making an illustration of non-periodic tiling chickens that were derived from the kites and darts similar to those M.C. Escher made for other polygons (Figure 12).
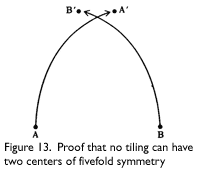
Penrose tilings, and in fact no tiling, can have more than one center of fivefold symmetry. John Horton Conway showed this, using a reductio ad absurdum proof, as follows. Assume a tiling has more than one center of fivefold symmetry. Take the two centers closest together, and label them A and B. Rotate the tiling around B by 72° (360/5) counterclockwise, carrying A to A′. Return to the original, and rotate the tiling around A by 72° clockwise, carrying B to B′. Since both are centers of symmetry, both rotations should leave the pattern unchanged. But now it has two centers of fivefold symmetry, A′ and B&prime, that are closer together than A and B, which contradicts the assumption that A and B are the closest centers (see Figure 13).
Robert Ammann was able to show that Penrose tilings had a 1-dimensional analogue with the Ammann Bars, and in 1976 he found a 3-dimensional analogue as well. He took a set of two rhombohedra, parallelepipeds with six congruent rhombus faces, and showed that with face-matching rules, they could tile space non-periodically. The two rhombohedra are golden rhombohedra, so that the faces have diagonals in the golden ratio. When Ammann’s discovery was made public, Penrose came to the conclusion that it might be a model for certain unexplainable molecular formations, such as viruses. He wrote in a letter to Martin Gardener “some viruses grow in the shapes of regular dodecahedra and icosahedra. It has always seemed puzzling how they do this. But with Ammann’s non-periodic solids as basic units, one would arrive at quasi-periodic ‘crystals’ involving such seemingly impossible (crystallographically) cleavage directions along dodecahedral or icosahedral planes. Is it possible that the viruses might grow in some such way involving non-periodic basic units—or is the idea too fanciful?” (Gardener 24) For many crystallographers, his ideas were too fanciful, for they contradicted rules that they had been following for over a century. These rules state that the units that make up a crystal must fall into an orderly, regular arrangement to fill up the space, and forbid non-periodic tiling.
In 1984, though, Dany Schechtman announced that he had found a non-periodic structure in metallic crystals composed of aluminum and manganese. The electron micrographs of this aluminum-manganese alloy clearly indicated a fivefold symmetry which “strongly suggested a nonperiodic space tiling analogous to Penrose tiling” (Gardener 25). Traditionally, crystal structures have a high degree of order and have periodic structures. This implies that, like tiling the plane with regular polygons, only triangular, square, or hexagonal lattices could fit the requirements for a crystalline structure. The key feature of quasicrystals, though, is that their atomic structure is not periodic. Atoms are not spaced at regular intervals in quasicrystals, but at long or short intervals. The Penrose tiling was important in the development of the possibility of quasicrystals, with each Penrose rhombus representing a cluster of atoms.
The Penrose model for quasicrystals was not wholly accepted, nor was it completely accurate. Linus Pauling argued that quasicrystal samples are really made up of twins, which are regular alone, but together create anomalous diffraction patterns. Also, the diffraction patterns were not as perfect as they should have been, implying that either the samples were flawed, or that the Penrose model is physically impossible to achieve.
Others worry about the use of tiles as models for atoms, since the conditions needed to form a Penrose tiling are far more complex than what is needed to form periodic crystals. Traditional crystals are composed of single building blocks, which are the atomic cluster with the lowest energy of the given elements. The Penrose model contains two building blocks, so there would need to be a balance of energy that would allow two different structures to co-exist. Then, the atomic interactions would need to restrict the clusters so they could only join in certain ways. Starting in 1989, though, quasicrystals have been found whose quasiperiodic order is as perfect as the periodic order found in traditional alloys, and are thermodynamically stable. So while the Penrose model has remained questionable from a theoretical standpoint, it has been increasingly supported experimentally.
A new way of constructing Penrose tilings was discovered in 1996 by Hyeong-Chai Jeong at the University of Maryland based on a construction by Petra Gummelt, an East German mathematician. Gummelt showed that it was possible to construct a non-periodic tiling using only a decagon as shown in Figure 14a, though it is not a conventional tiling in the sense that neighboring tiles overlap (Figure 14b).
The overlapping areas must match in color, and the hexagonal area shown in Figure 14b.1 must be covered, so only the two types of overlaps shown in Figure 14B are allowed. The decagonal tiling shown in Figure 15 can be mapped to a Penrose tiling by inscribing a fat Penrose rhombus in each Decagon as shown in Figure 14c. The coloring of the decagons insures that this mapping conforms to the mapping rules for a Penrose tiling.
Gummelt’s work has had a great impact on physicists working with quasicrystals. For one, it shows that the crystals can be built using a single building block, instead of the two in the original model. The point that two co-existing structures is highly improbable becomes moot from this discovery. Also, since atomic structures are not exactly like tiles, the overlapping nature of Gummelt’s tiling can be interpreted as the sharing of atoms by clusters, which has been observed in quasicrystals.